# HashMap源码&底层数据结构分析
# HashMap 简介
HashMap 主要用来存放键值对,它基于哈希表的 Map 接口实现,是常用的 Java 集合之一,是非线程安全的。
HashMap 可以存储 null 的 key 和 value,但 null 作为键只能有一个,null 作为值可以有多个
JDK1.8 之前 HashMap 由 数组+链表 组成的,数组是 HashMap 的主体,链表则是主要为了解决哈希冲突而存在的(“拉链法”解决冲突)。 JDK1.8 以后的 HashMap 在解决哈希冲突时有了较大的变化,当链表长度大于阈值(默认为 8)(将链表转换成红黑树前会判断,如果当前数组的长度小于 64,那么会选择先进行数组扩容,而不是转换为红黑树)时,将链表转化为红黑树,以减少搜索时间。
HashMap 默认的初始化大小为 16。之后每次扩充,容量变为原来的 2 倍。并且, HashMap 总是使用 2 的幂作为哈希表的大小。
# 底层数据结构分析
HashMap类属性
public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable {
// 序列号
private static final long serialVersionUID = 362498820763181265L;
// 默认的初始容量是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
// 默认的填充因子
static final float DEFAULT_LOAD_FACTOR = 0.75f;
// 当桶(bucket)上的结点数大于这个值时会转成红黑树
static final int TREEIFY_THRESHOLD = 8;
// 当桶(bucket)上的结点数小于这个值时树转链表
static final int UNTREEIFY_THRESHOLD = 6;
// 桶中结构转化为红黑树对应的table的最小容量
static final int MIN_TREEIFY_CAPACITY = 64;
// 存储元素的数组,总是2的幂次倍
transient Node<k,v>[] table;
// 存放具体元素的集
transient Set<map.entry<k,v>> entrySet;
// 存放元素的个数,注意这个不等于数组的长度。
transient int size;
// 每次扩容和更改map结构的计数器
transient int modCount;
// 临界值(容量*填充因子) 当实际大小超过临界值时,会进行扩容
int threshold;
// 加载因子
final float loadFactor;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
loadFactor 加载因子
loadFactor 加载因子是控制数组存放数据的疏密程度,loadFactor 越趋近于 1,那么 数组中存放的数据(entry)也就越多,也就越密,也就是会让链表的长度增加,loadFactor 越小,也就是趋近于 0,数组中存放的数据(entry)也就越少,也就越稀疏。
loadFactor 太大导致查找元素效率低,太小导致数组的利用率低,存放的数据会很分散。loadFactor 的默认值为 0.75f 是官方给出的一个比较好的临界值。
给定的默认容量为 16,负载因子为 0.75。Map 在使用过程中不断的往里面存放数据,当数量达到了 16 * 0.75 = 12 就需要将当前 16 的容量进行扩容,而扩容这个过程涉及到 rehash、复制数据等操作,所以非常消耗性能。
threshold
threshold = capacity * loadFactor,当 Size>=threshold的时候,那么就要考虑对数组的扩增了,也就是说,这个的意思就是 衡量数组是否需要扩增的一个标准。
Node 节点类
// 继承自 Map.Entry<K,V>
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;// 哈希值,存放元素到hashmap中时用来与其他元素hash值比较
final K key;//键
V value;//值
// 指向下一个节点
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
// 重写hashCode()方法
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
// 重写 equals() 方法
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
树节点类源码:
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // 父
TreeNode<K,V> left; // 左
TreeNode<K,V> right; // 右
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red; // 判断颜色
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
// 返回根节点
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# HashMap 源码分析
# 构造方法
HashMap 中有四个构造方法,它们分别如下:
// 默认构造函数。
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
// 包含另一个“Map”的构造函数
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);//下面会分析到这个方法
}
// 指定“容量大小”的构造函数
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
// 指定“容量大小”和“加载因子”的构造函数
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
putMapEntries 方法
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
int s = m.size();
if (s > 0) {
// 判断table是否已经初始化
if (table == null) { // pre-size
// 未初始化,s为m的实际元素个数
float ft = ((float)s / loadFactor) + 1.0F;
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
// 计算得到的t大于阈值,则初始化阈值
if (t > threshold)
threshold = tableSizeFor(t);
}
// 已初始化,并且m元素个数大于阈值,进行扩容处理
else if (s > threshold)
resize();
// 将m中的所有元素添加至HashMap中
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# put 方法
HashMap 只提供了 put 用于添加元素,putVal 方法只是给 put 方法调用的一个方法,并没有提供给用户使用。
对 putVal 方法添加元素的分析如下:
- 如果定位到的数组位置没有元素 就直接插入。
- 如果定位到的数组位置有元素就和要插入的 key 比较,如果 key 相同就直接覆盖,如果 key 不相同,就判断 p 是否是一个树节点,如果是就调用
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value)将元素添加进入。如果不是就遍历链表插入(插入的是链表尾部)。
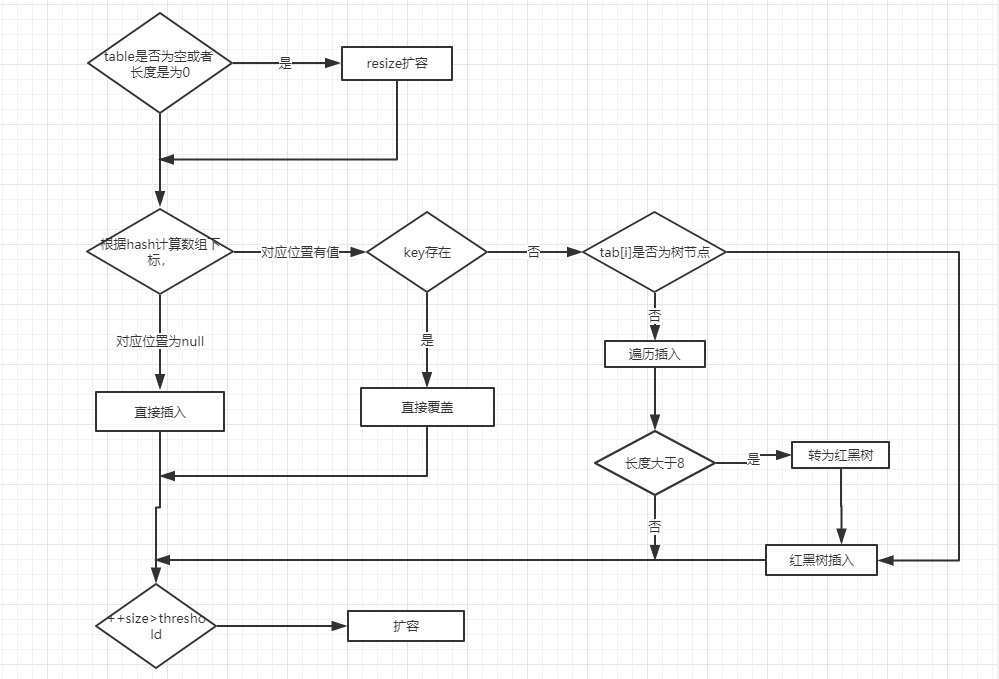
说明:上图有两个小问题:
- 直接覆盖之后应该就会 return,不会有后续操作。参考 JDK8 HashMap.java 658 行(issue#608 (opens new window))。
- 当链表长度大于阈值(默认为 8)并且 HashMap 数组长度超过 64 的时候才会执行链表转红黑树的操作,否则就只是对数组扩容。参考 HashMap 的
treeifyBin()方法(issue#1087 (opens new window))。
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// table未初始化或者长度为0,进行扩容
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n - 1) & hash 确定元素存放在哪个桶中,桶为空,新生成结点放入桶中(此时,这个结点是放在数组中)
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// 桶中已经存在元素(处理hash冲突)
else {
Node<K,V> e; K k;
// 判断table[i]中的元素是否与插入的key一样,若相同那就直接使用插入的值p替换掉旧的值e。
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 判断插入的是否是红黑树节点
else if (p instanceof TreeNode)
// 放入树中
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 不是红黑树节点则说明为链表结点
else {
// 在链表最末插入结点
for (int binCount = 0; ; ++binCount) {
// 到达链表的尾部
if ((e = p.next) == null) {
// 在尾部插入新结点
p.next = newNode(hash, key, value, null);
// 结点数量达到阈值(默认为 8 ),执行 treeifyBin 方法
// 这个方法会根据 HashMap 数组来决定是否转换为红黑树。
// 只有当数组长度大于或者等于 64 的情况下,才会执行转换红黑树操作,以减少搜索时间。否则,就是只是对数组扩容。
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
// 跳出循环
break;
}
// 判断链表中结点的key值与插入的元素的key值是否相等
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// 相等,跳出循环
break;
// 用于遍历桶中的链表,与前面的e = p.next组合,可以遍历链表
p = e;
}
}
// 表示在桶中找到key值、hash值与插入元素相等的结点
if (e != null) {
// 记录e的value
V oldValue = e.value;
// onlyIfAbsent为false或者旧值为null
if (!onlyIfAbsent || oldValue == null)
//用新值替换旧值
e.value = value;
// 访问后回调
afterNodeAccess(e);
// 返回旧值
return oldValue;
}
}
// 结构性修改
++modCount;
// 实际大小大于阈值则扩容
if (++size > threshold)
resize();
// 插入后回调
afterNodeInsertion(evict);
return null;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
对比一下 JDK1.7 put 方法的代码
public V put(K key, V value)
if (table == EMPTY_TABLE) {
inflateTable(threshold);
}
if (key == null)
return putForNullKey(value);
int hash = hash(key);
int i = indexFor(hash, table.length);
for (Entry<K,V> e = table[i]; e != null; e = e.next) { // 先遍历
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(hash, key, value, i); // 再插入
return null;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- 1、如果定位到的数组位置没有元素 就直接插入。
- 2、如果定位到的数组位置有元素,遍历以这个元素为头结点的链表,依次和插入的 key 比较,如果 key 相同就直接覆盖,不同就采用头插法插入元素。
# get 方法
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// 数组元素相等
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 桶中不止一个节点
if ((e = first.next) != null) {
// 在树中get
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// 在链表中get
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# resize 方法
进行扩容,会伴随着一次重新 hash 分配,并且会遍历 hash 表中所有的元素,是非常耗时的。在编写程序中,要尽量避免 resize。
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
// 超过最大值就不再扩充了,就只好随你碰撞去吧
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 没超过最大值,就扩充为原来的2倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else {
// signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 计算新的resize上限
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// 把每个bucket都移动到新的buckets中
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else {
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
// 原索引
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
// 原索引+oldCap
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 原索引放到bucket里
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
// 原索引+oldCap放到bucket里
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81